角边角定理(角边角定理怎么推导出来的)

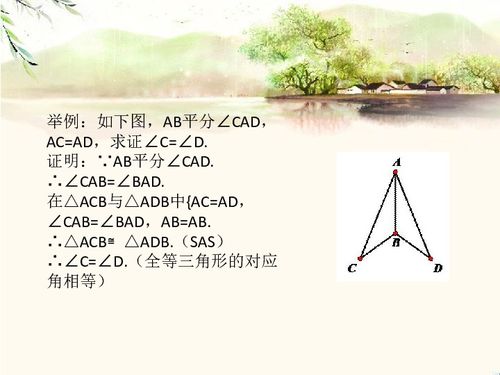
角边角定理是几何学中的一个基本定理，它指出三角形的一个内角等于与它不相邻的两个内角的和。这个定理的重要性在于它为三角形的内角和定理奠定了基础，同时也为解决一些几何问题提供了重要的思路。

什么是角边角定理?

角边角定理是指在一个三角形中，有一个内角A，另外两个内角B和C，满足A+B+C=180°。如果另外两条边分别为a、b，连接这两个角的边分别为c、d，那么有A=B=C=180°-D，其中D为角A的对边。

角边角定理的重要性

角边角定理的重要性在于它为三角形的内角和定理奠定了基础。任何一个三角形的内角和都可以用180°来表示，而角边角定理则给出了一个计算内角和的方法。另外，角边角定理也为解决一些几何问题提供了重要的思路，例如求解一个凸多边形的内角和、求解一个内角为150°的三角形等。

如何应用角边角定理?

角边角定理可以用于解决许多几何问题，下面列举一些常见的应用场景： 1. 计算一个凸多边形的内角和：设一个凸多边形有n条边，那么它的内角和可以表示为(n-2)×180°。但是，这个公式比较复杂，而角边角定理可以简化计算过程。 2. 求解一个内角为150°的三角形：设一个三角形的三个内角分别为A、B、C，且A=150°，那么根据角边角定理，有B+C=30°。又因为三角形内角和为180°，所以A+B+C=180°，解得B=C=45°。 3. 求解一个内角为30°的三角形：设一个三角形的三个内角分别为A、B、C，且A=30°，那么根据角边角定理，有B+C=150°。又因为三角形内角和为180°，所以A+B+C=180°，解得B=C=120°。

角边角定理的实际应用

角边角定理在实际生活中有广泛的应用，下面列举一些实际应用场景： 1. 设计一个建筑：在建筑设计中，需要考虑到各个角度和边长，而角边角定理可以帮助计算出建筑各个角度和边长，从而设计出更加完美的建筑。 2. 求解一个电子电路：在电子电路中，需要考虑到各个元件之间的连接和角度，而角边角定理可以帮助计算出电子电路中各个元件之间的角度和边长，从而确保电路的正常工作。 3. 解决一个谜题：有些谜题需要通过计算来解决，而角边角定理可以帮助计算出一些谜题的答案。

如何证明角边角定理?

角边角定理可以通过以下方式证明： 证明：在一个三角形中，有一个内角A，另外两个内角B和C，满足A+B+C=180°。如果另外两条边分别为a、b，连接这两个角的边分别为c、d，那么有A=B=C=180°-D，其中D为角A的对边。我们需要证明A=B=C=180°-D。 证明过程： 由于三角形内角和为180°，所以A+B+C=180°。 又因为另外两条边分别为a、b，连接这两个角的边分别为c、d，所以有A=B=C=180°-D，其中D为角A的对边。 根据三角形内角和定理，可以得到A+B+C=180°，即A=B=C=180°-D。 因此，我们证明了角边角定理。