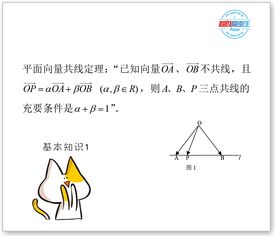
向量共面定理(向量共面定理公式)

向量共面定理：

1. 基本概念

向量共面定理是线性代数中一个重要的定理，它指出两个向量共面的充要条件是它们可以表示为一个标量与另一个向量的乘积。共面定理在向量空间中有着广泛的应用，它可以帮助我们简化向量的运算，提高问题的求解效率。 向量共面定理的向量表示：

2. 向量共面定理的向量表示

向量共面定理的向量表示是一个重要的概念，它将向量与向量之间的关系用向量表示出来。设向量 $\overrightarrow{a}$ 和向量 $\overrightarrow{b}$ 共面，则存在一个标量 $λ$，使得 $\overrightarrow{a}=λ\overrightarrow{b}$。这个 $λ$ 称为向量 $\overrightarrow{a}$ 和向量 $\overrightarrow{b}$ 的共面系数。 向量共面定理的向量共面：

3. 向量共面定理的向量共面

向量共面定理指出，如果两个向量共面，则它们可以表示为一个标量与另一个向量的乘积。具体来说，如果 $\overrightarrow{a}$ 和 $\overrightarrow{b}$ 共面，则存在一个标量 $λ$，使得 $\overrightarrow{a}=λ\overrightarrow{b}$。这个 $λ$ 称为向量 $\overrightarrow{a}$ 和向量 $\overrightarrow{b}$ 的共面系数。 向量共面定理的向量运算：

4. 向量共面定理的向量运算

向量共面定理在向量运算中有着广泛的应用。假设向量 $\overrightarrow{a}$ 和向量 $\overrightarrow{b}$ 共面，则可以对向量 $\overrightarrow{a}$ 和向量 $\overrightarrow{b}$ 进行线性运算，如加法、数乘等。这些运算都可以用向量共面定理表示出来，使得运算更加简便。 向量共面定理的实际应用：

5. 向量共面定理的实际应用

向量共面定理在实际应用中有着广泛的应用，如在图形处理中、在物理学中、在计算机图形学中等等。通过向量共面定理，我们可以简化向量的运算，提高问题的求解效率。 向量共面定理的数学证明：

6. 向量共面定理的数学证明

向量共面定理的数学证明是通过向量空间的概念来实现的。向量空间是一种抽象的结构，它将向量与向量之间的关系用向量表示出来。在向量空间中，向量共面定理可以被证明为：两个向量共面的充要条件是它们可以表示为一个标量与另一个向量的乘积，其中这个标量称为向量 $\overrightarrow{a}$ 和向量 $\overrightarrow{b}$ 的共面系数。